What is DassFlow ?
DassFlow (Data Assimilation for Free Surface Flows) denotes a set of computational codes aiming at modeling free surface geophysical flows (water-rivers, ice-glaciers, lavas, muds etc) with data assimilation capabilities. The flow models are mainly shallow-water types (long-wave assumption, non turbulent).
Three different codes exist: DassFlow-2D, DassFlow-1D and DassFlow-Py.
The kernel codes are written in Fortran for DassFlow-2D and DassFlow-1D. Latest versions of these two codes are wrapped in Python, therefore enabling easy the use of other Python libraries. DassFlow-Py is fully written in Python.
*
Update. DassFlow is now part of DassHydro (Data Assimilation for Hydrology) plateform.
DassHydro includes DassFlow and SMASH (INRAe et al.) thus providing a complete computational plateform dedicated to hydrology (floods, inundations).
DassFlow and SMASH are built following the same technologies: Fortran kernel codes, Python wrapping, providing Data Assimilation capabilities.
To have a look to the applications, rivers, hydrology and the HiVDI (Hierarchical Variational Discharge Inference) algorithm (spatial hydrology), go to the "rivers" page (menu on the left).
For glaciology (DassFlow applications only), go to "glaciers" page.
For a description of the basic codes ingredients, the description below should interest you.
Features
Fluid flow models & numerical schemes.
The dynamics flow models are a mix of classical ones and original ones.
DassFlow-1D: 1D SWE (St-Venant) in variables (S,Q)(x,t), diffusive wave equations (the standard one and an original two-scales one). Multi-branches (network) is possible.
DassFlow-2D: the 2D SWE in variables (h,q)(x,y,t). (Full 2D flows or 1D-like branches with 2D zooms possible).
Additional original models dedicated to spatial hydrology inverse problems are available: low-Froude algebraic systems (rivers).
Complex network mixing 1D parts with integrated 2D zooms are handled (with the complete inverse capabilities) therefore enabling complex river networks modeling.
Moreover, DassFlow-2D integrates hydrological models (spatially distributed or not) developed at INRAe: the so-called models GR4 and SMASH.
Herschel-Bulkley rheology is available too (e.g. lavas, mud flows).
DassFlow-Py: 2d shallow non Newtonian fluid flows models (power-law, Herschel-Bulkley, also a Reduced Uncertainty glaciers dynamics model (RU-SIA).
Numerical schemes. The numerical schemes are a mix of classical ones and original ones. They are Finite Volume schemes (1st order/2nd order) for shallow flow models and Finite Element schemes (2nd order) (2 fields or 4 fields) for Stokes like models (with power law rheology).
Boundary conditions required for real-world flows are available.
Meshes: mix of triangles-quadrangles for 2D FV schemes; triangles, quadrangles and tetrahedron for FE (both 2D and 3D solvers are available).
Inverse problems: Variational Data Assimilation (VDA) & Deep Learning.
An important feature of DassFlow codes are their capabilities to address inverse problems, in particular by VDA (adjoint-based method). Since the Python wrapped versions, combining VDA method (physics-based methoid) with Deep Learning (purely data driven estimations) is much easier.
VDA aims at minimizing the difference between the model output and data (cost function). The gradient of the cost function is computed by deriving an adjoint code (obtained by algorithmic differenciation or not). The complete optimization process provides parameters identification, reduced uncertainties, calibrated model(s). VDA formulations are based on priors: first guess values and covariances operators (probabilistic priors).
Classical and original covariances operators are available. Different regularization terms can be easily introduced.
Gradients computation and optimization algorithms.
For VDA, the gradients are computed using the adjoint method. The adjoint codes are generated either using the Automatic Differentiation tool Tapenade (INRIA) or by coding the adjoint equations.
Optimization routines (1st order methods) are either the ones from NumPy library or the L-BFGS quasi-Newton algorithm M1QN3 (from INRIA).
Local sensitivities are available by plotting the gradients (spatially distributed gradient values).
Assimilated data can be combinations of in-situ and remote-sensed observations, either time-series and/or spatially distributed.
A twin experiment mode (generation next inversions of synthetic data) is available.
Numerous benchmarks are available both for the forward models and the inverse ones.
Python wrapped versions can be easily interfaced/coupled with other Python libraries eg deep learning ones etc.
Reduced Order Models (ROMs) are in development.
Extra capabilities:
- Assimilation of Lagrangian data e.g. extracted from video images. This feature should be re-activated soon.
-DassFlow-3d: 3D Stokes flow power-law rheology with mobile free-surface (ALE formulation if 2D vertical).
The different code versions
DassFlow platform includes the following computational codes : DassFlow-2d (2D Shallow-Water, Newtonian or not, FV schemes), DassFlow-1d (Saint-Venant, FV and FD schemes, Diffusive Wave equations).
Two others separated versions are: DassFlow-py (Ice-lava flows models, multi-regimes, 2D shallow; FE schemes). DassFlow-3d (Stokes like systems -power law rheology, low inertia, FE schemes).
A description of each code version is available on the versions page.
Codes langages and architectures
DassFlow-1D and DassFlow-2D kernel codes are written in Fortran 90 (MPI for the 2D version). Moreover, these Fortran computational kernels are wrapped in Python. This enables to complete these physics-based computations with other Python libraries. The latter can be simple pre or post-processing of the computed fields or data, Artificial Neural Networks, wavelet basis etc ; also UQ libraries such as OpenTurns, etc.
Linear systems are solved using MUMPS or NumPy libraries.
Each code version includes the forward code (FE or FV schemes, 1st and/or 2nd order), the corresponding adjoint code (source code differenciation or not) and gradient-based optimization algorithms.
Each code version is interfaced with few (free or commercial) pre and post-processors (SIG tools, mesh generators, visualization
tools) enabling to address real-world datasets.
DassFlow is developed under the CeCILL licence.
Funding history.
The various developments have been co-funded by INSA Toulouse - CNRS (since 2008), next Group INSA and CNES (since 2014). It has been co-funded by the French agency ANR too (projects 2009-13, 2022-26).
The ancient basic version (not available anymore) has been funded by the Grenoble Institute of Technology INPG, by Région Rhône-Alpes (research project
"Numerical prediction for floods", 2003-06), and by INRIA Rhône-Alpes (code under licence APP).

|
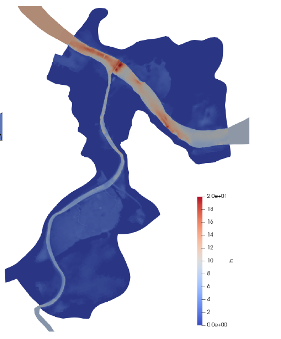
Application in hydrology / DassFlow-2D. Multi-D hydrological-hydraulic modeling, with data assimilation. Adour basin (soout-western France) (Up) with a zoom on Bayonne city (water depth h in m) (Down).
Image L. Pujol's PhD. Computations ICUBE-INRAe-INSA/IMT (data SPC).
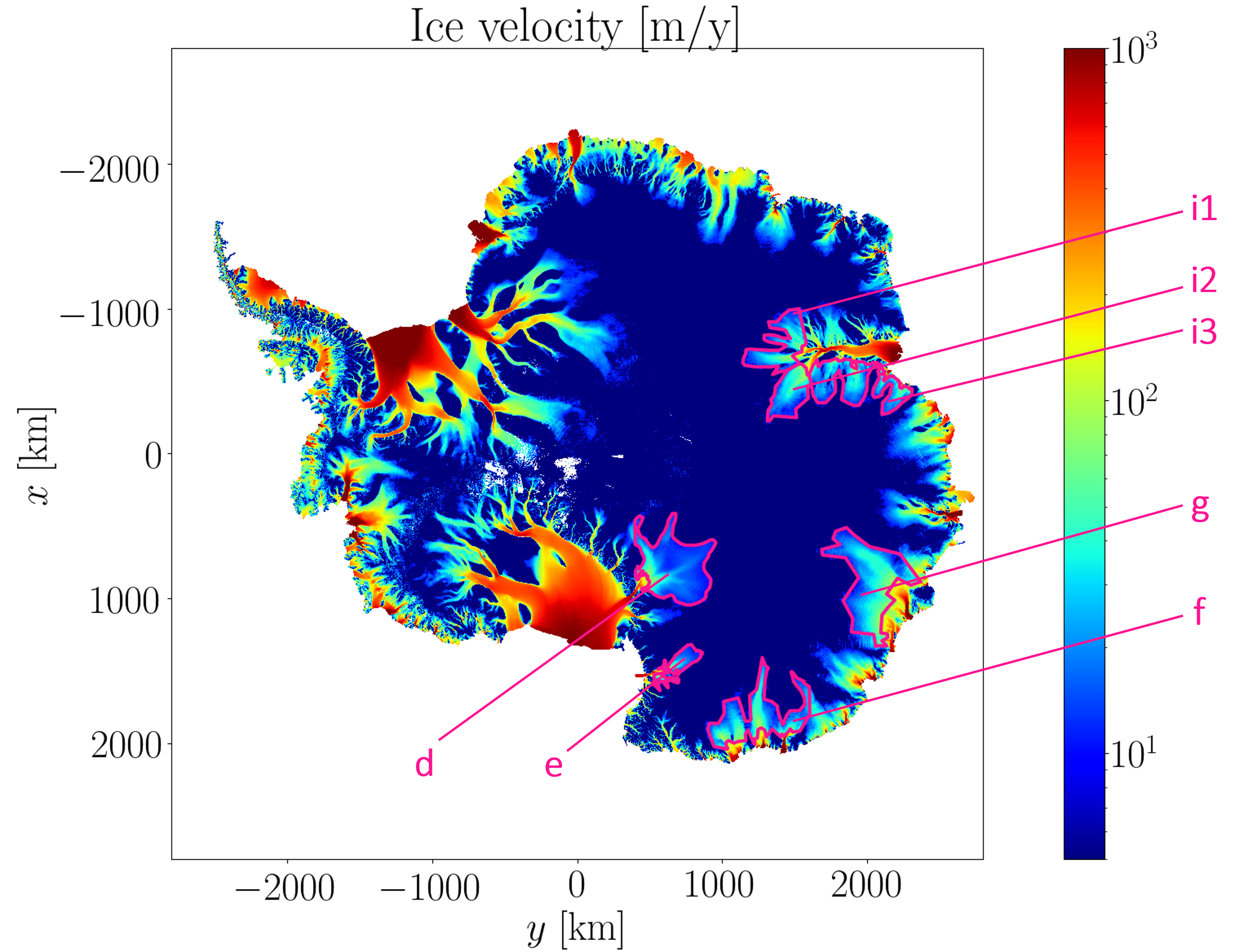
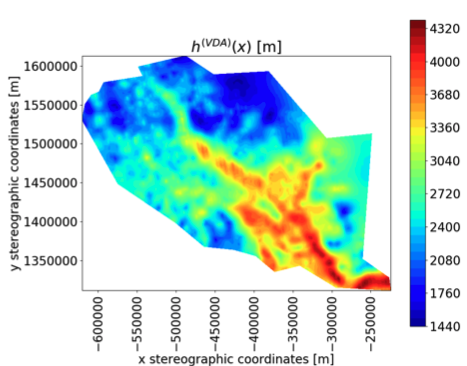
Application in glaciology / DassFlow-Py. Estimation of bedrock elevation beneath glaciers in poorly measured / moderatly fast ice flows regions in East Antarctica (L). Zoom on i2 area (ice thickness h in m) (R). Computations INSA/IMT (international open datasets).
|