Discrete-time Derrida-Retaux Model
The Derrida-Retaux model has first been introduced as a discrete-time process defined recursively as follows. Let \(X_0\) be a random variable, which is our initial condition. Then, for any \(n \geq 0\), we define \(X_{n+1} = \max(X_n+\overline{X}_n-1,0)\), where \(\overline{X}_n\) is an independent copy of \(X_n\).
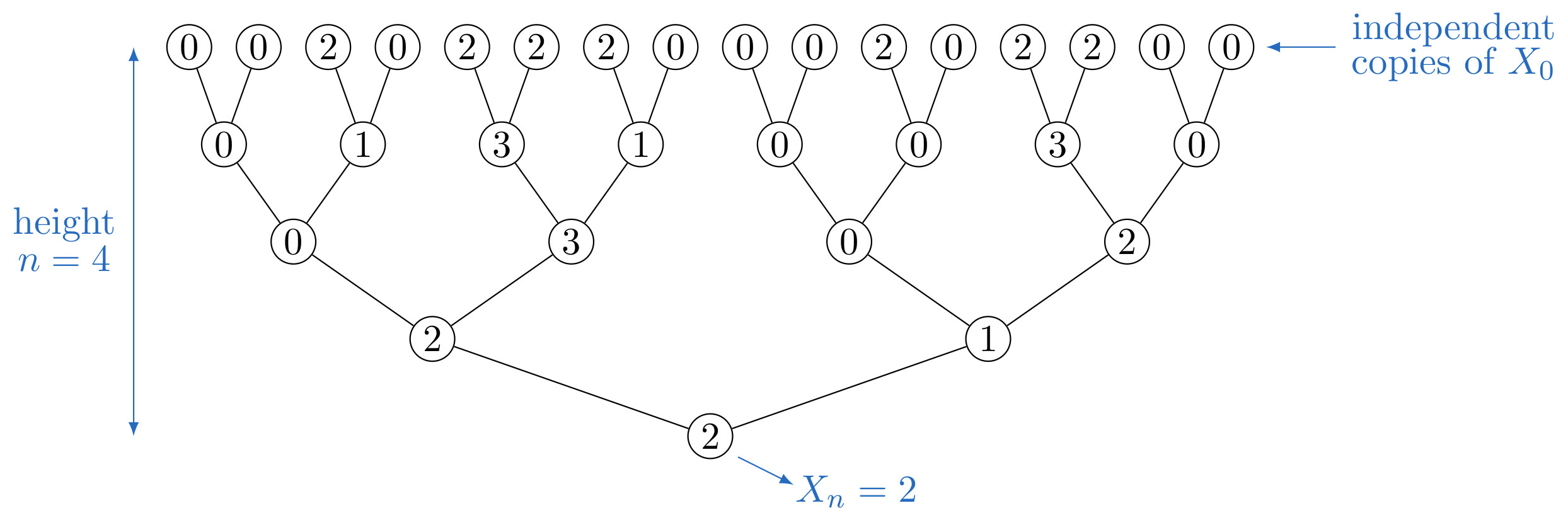
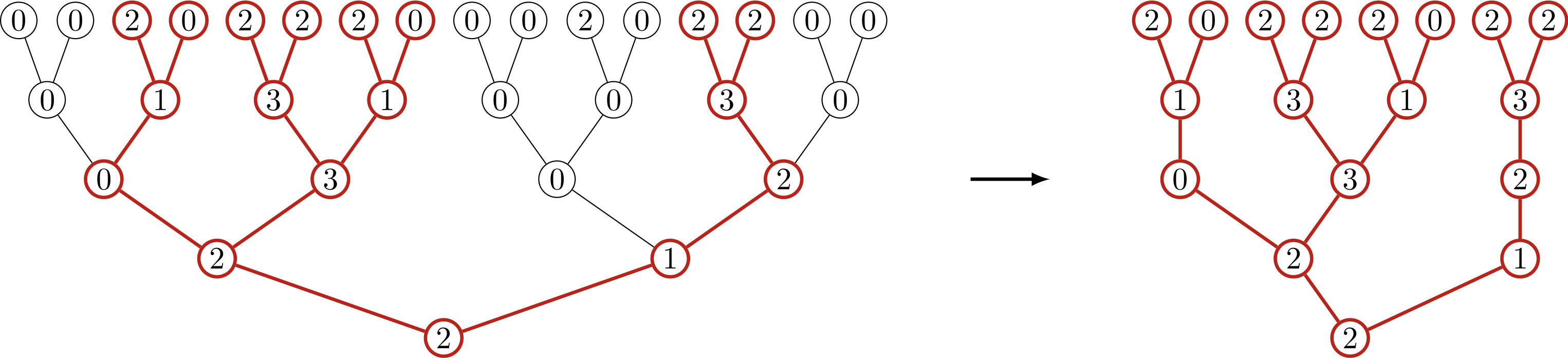
The random variable \(X_n\) can also be defined using a binary tree of height \(n\) and attributing values to its nodes as follows. The values of the leaves are independent copies of \(X_0\). Then, we proceed toward the root in a deterministic way: any node whose children have values \(a\) and \(b\) is given the value \(\max(a+b-1,0)\). The value of the root gives \(X_n\). This procedure is illustrated on the following picture, where the initial condition \(X_0\) takes values \(0\) and \(2\).
This process exhibits a phase transition. For simplicity, assume \(X_0\) takes value \(2\) with probability \(p\) and value \(0\) otherwise. Then, the following limit exists \[F(p) = \lim_{n\to\infty} \frac{\mathbb{E}[X_n]}{2^n},\] and is called the free energy of the system. Then two phases appear: \[\begin{cases}F(p) = 0 & \text{if} & p \leq p_c & \text{(subcritical phase)}, \\ F(p) > 0 & \text{if} & p > p_c & \text{(supercritical phase)},\end{cases}\] where \(p_c = 1/5\) in our particular example. In the subcritical phase (\(p \leq p_c\)), one even has \(X_n \to 0\) almost surely, which shows a drastic change of behavior. Moreover, the phase transition is of infinite order: the function \(F(p)\) is infinitely divisible at the critical point \(p_c\), see the picture below.
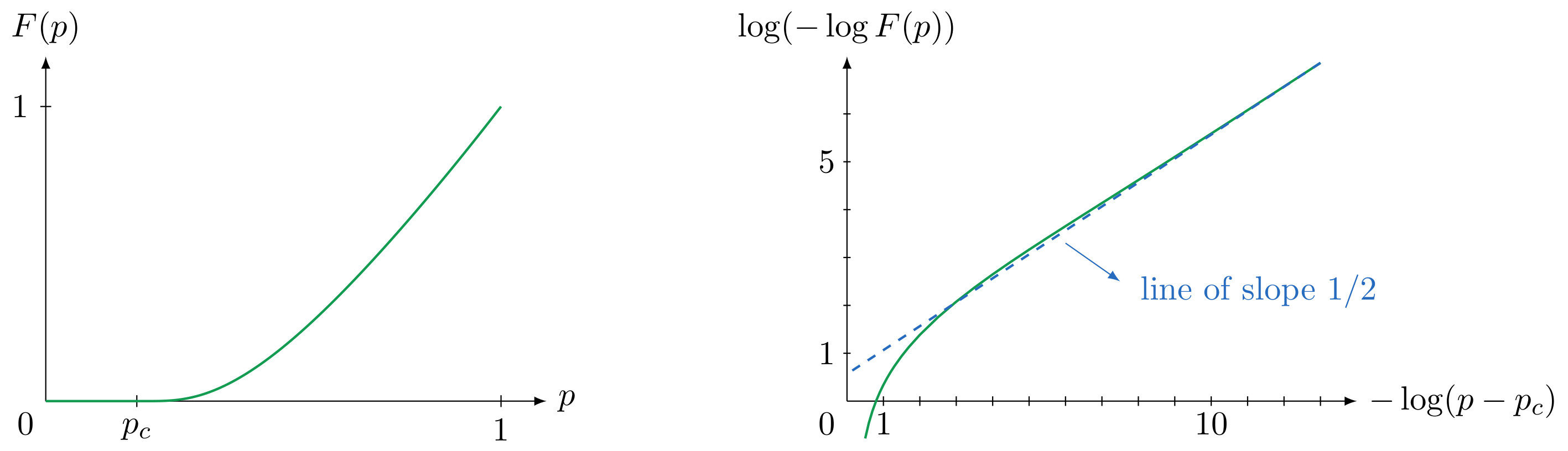
The precise behavior of the free energy close to criticality is \[F(p) = \exp \left( - \frac{1}{(p-p_c)^{1/2+o(1)}} \right),\qquad \text{as } p \downarrow p_c,\] as conjectured by Derrida and Retaux and proved recently by Chen, Dagard, Derrida, Hu, Lifshits and Shi for integer valued intial conditions.
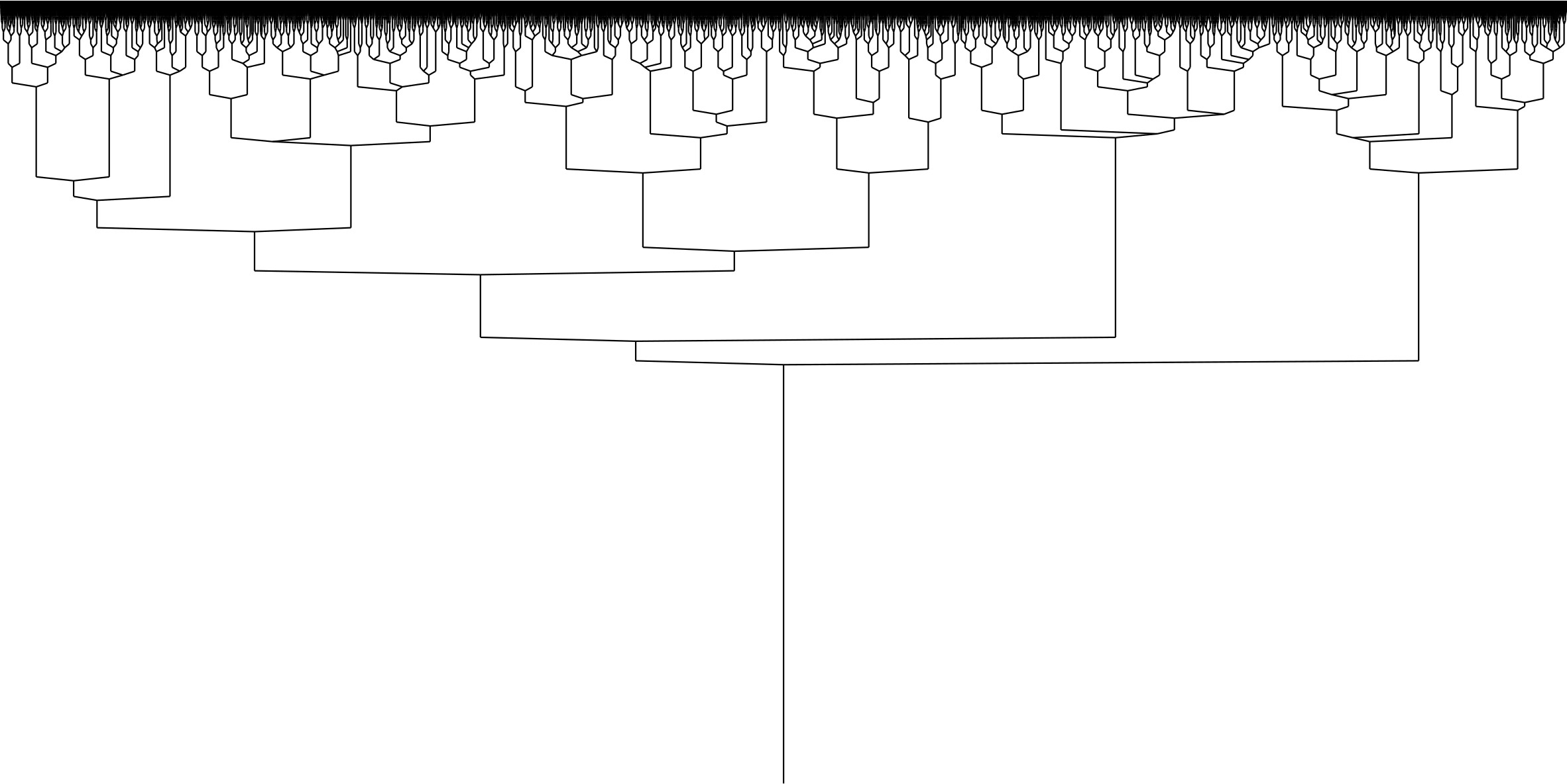
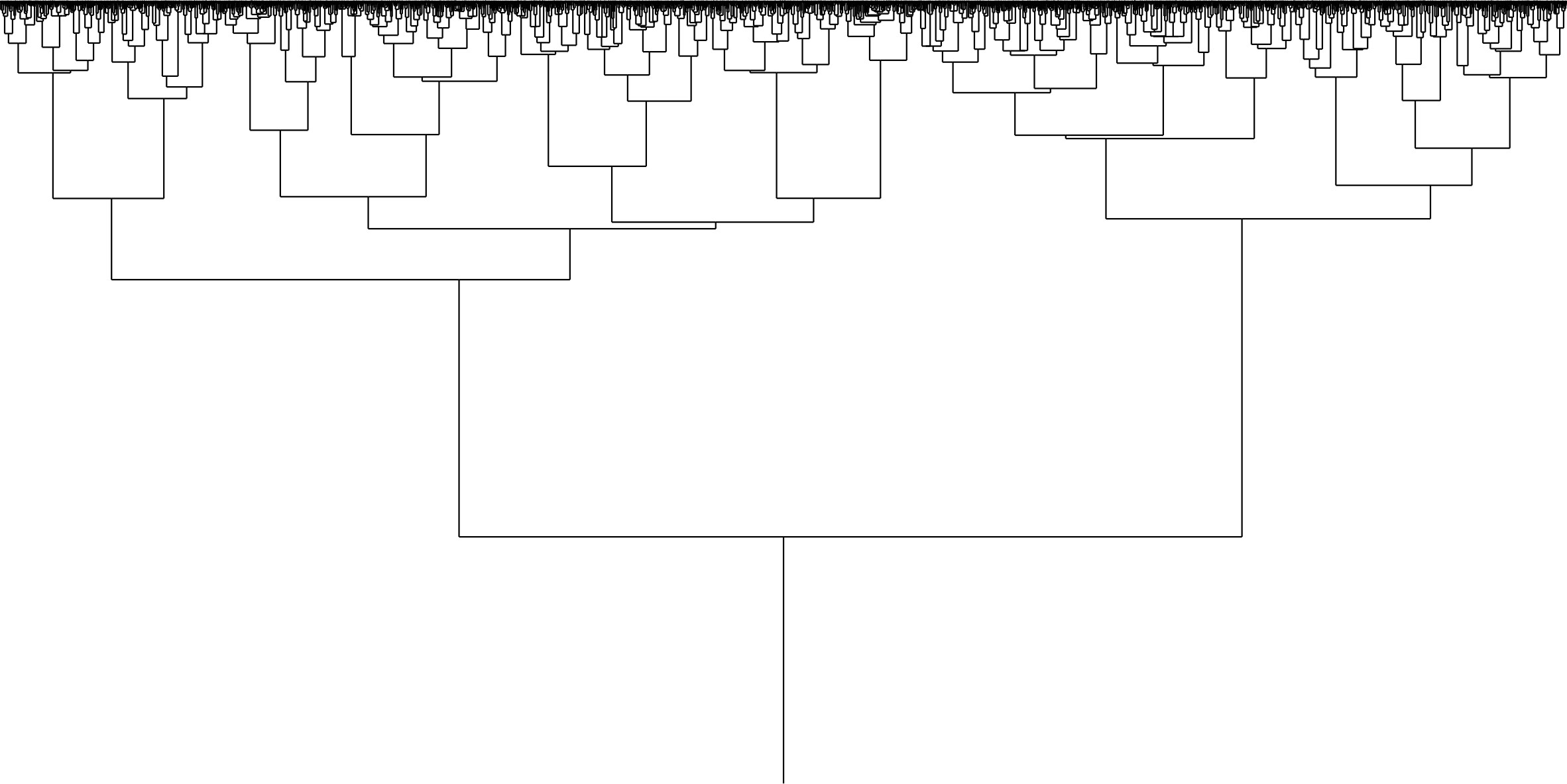
The critical case \(p=p_c\) is supposed to exhibit universal behaviors. One way to understand it precisely is to study the so-called red tree, defined as follows. For some fixed \(n\), given that \(X_n>0\), we color in red paths from a leaf to the root if the operation of taking the maximum with \(0\) is never used along it. The union of these paths defines a subtree, called the red tree, see the picture below.
Below is a simulation of the red tree with \(n=200\). Starting from the root, the first branching times are of order \(n\). The number of red leaves is conjectured to be of order \(n^2\) and the red tree should converge toward a universal limit introduced for the continuous Derrida-Retaux model discussed below.