La cascade de doublements de période : la constante de Feigenbaum

Décrivons ce qui se passe :

Quand le paramètre part de a = 1 et augmete progressivement, l'attracteur, qui est un point, bouge. Arrivé à a = 3, il se scinde en deux points qui s'éloignent rapidement. Arrivé à a = 3.449…, chacun de ces deux points se scinde à nouveau en deux, donnant ainsi un attracteur à 4 points. Arrivé à a = 3.544…, il y a à nouveau un doublement, la période passant à 8. Et ainsi de suite… a = 3.564… donne 16 points, a = 3.569 en donne 32, etc.

La suite des valeurs des paramètres où a lieu le dédoublement de période est noté a₀, a₁, a₂, …. Elle est illustrée sur l'image suivante :

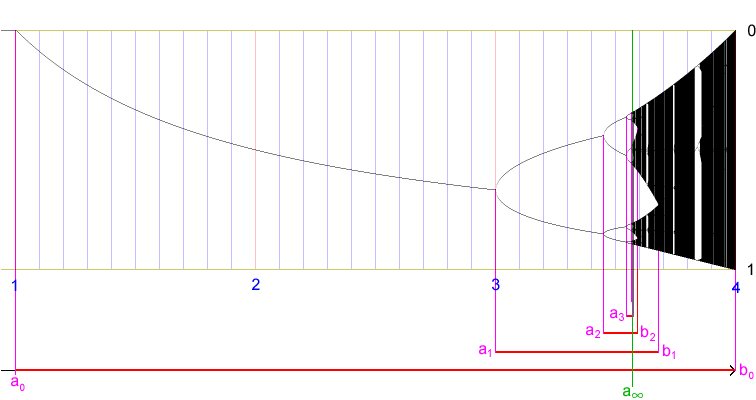
La suite a₀, a₁, a₂, … est croissante et tend vers une limite a_∞ = 3.570… (qui a probablement une infinité de décimales). Chaque nombre a_i est la borne d'un intervalle de paramètres [a_i,b_i] sur lequel f est renormalisable de période 2ⁱ. Plus précisément, f est renormalisable avec période 2 sur l'intervalle [a₁,b₁], appelé fenêtre, dans les pages précédentes. Au dessus de cet intervalle, se trouvent deux copies de l'arbre de Feigenbaum. Ces copies possèdent elles-mêmes une fenêtre [a₂,b₂] de période 2 pour la renormalisée, donc de période 4 pour f, qui correspond à la copie de l'intervalle [a₁,b₁] par la correspondance a ↦ b (où f : x ↦ a·x·(1−x) et où la renormalisée de f est conjuguée à x ↦ b·x·(1−x)). Et ainsi de suite…

Les distances d_i = a_i+1 - a_i entre deux a_i successifs tendent vers 0, et le quotient q_i = d_i / d_i+1 entre deux distances successives tend vers un nombre

delta = 4.6692… appelé constante de Feigenbaum.

C'est une constante universelle, car le phénomène de doublement de période est présent dans une très large classe de familles fonctions ayant la même allure que la famille a·x·(1−x) (par exemple des bouts de sinus, ou encore les renormalisées d'une fenêtre de la famille a·x·(1−x)), et si les valeurs des a_i ne sont pas forcément les mêmes, les quotients des distances les séparant tendent vers la même limite. La démonstration de ces affirmations est longue et emploie des techniques élaborées des mathématiques (analyse fonctionnelle).