Les fenêtres, les cas infiniment/finiment/non renormalisables

Conséquences de la renormalisation

Les "fenêtres"

Notons que les images de l'arbre de Feigenbaum sur cette page sont tournées de 90 degrés.

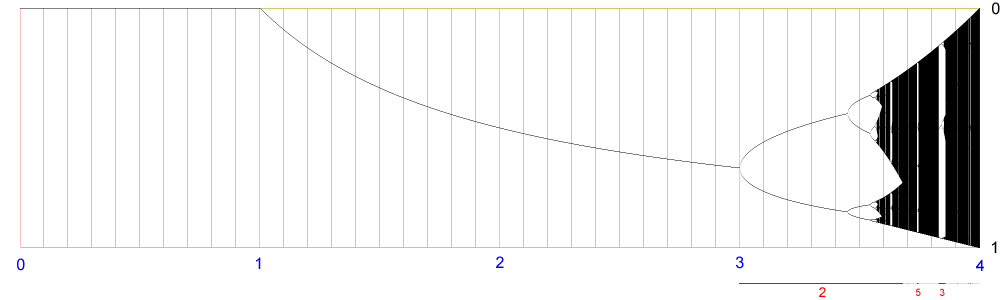
Déroulez pour la suite de l'image -->

L'ensemble des paramètres a tels que f : x ↦ a·x·(1−x) est renormalisable, est la réunion d'une infinité d'intervalles de paramètres de plus en plus petits. Pour des raisons que nous cachons, nous ne considérerons comme valide que les renormalisations pour lesquelles la renormalisée possède deux points fixes (cette renormalisée étant conjuguée à une certaine fonction x ↦ b·x·(1−x), cela équivaut à demander que b>1). Sur chacun de ces intervalles de paramètres, la période p renormalisation de f est la même (plus précisément la plus petite période de renormalisation, car une fonction peut être plusieurs fois renormalisable), ainsi que l'ordre dans lequel s'envoient les uns sur les autres les intervalles dynamiques de renormalisation de f. Notez que nous distinguons les intervalles de paramètre, concernant a, et les intervalles dynamiques, concernant x. Les intervalles paramétriques de renormalisation sont appelés fenêtres. Dans une fenêtre on observe p copies de l'arbre de Feigenbaum, s'étendant sur tout l'intervalle de paramètres. Ces copies sont déformées, et éventuellement retournées selon l'axe dynamique. Elles correspondent chacune à un des intervalles dynamiques délimitant un carré où le graphe de f^p est renormalisable.

Note : la plupart des affirmations précédentes sont difficiles à démontrer.

Les deux images suivantes illustrent un zoom sur une copie. La première est une reprise de l'image précédente, de a=3.4 (approximativement) à a=4, mais avec une échelle horizontale plus étendue. L'image est donc étirée. Un petit cadre violet entoure une copie. La deuxième est un zoom sur cette copie. On observe une forte ressemblance avec l'arbre initial, ainsi qu'un retournement. Notons que des nombreuses fenêtre dans les deux bandes noires entourant la copie sont invisibles, car trop petites sur le dessin.

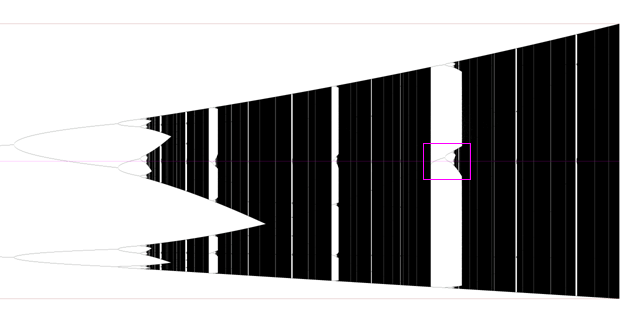
Voici une image deux-fois plus étirée. On y voit apparaître des fenêtres que l'on ne voyait pas sur la première image. Le phénomène est général : plus on zoome plus on en voit. En effet la réunion de tous les intervalles paramétriques de renormalisation est dense dans l'intervalle [3,4]

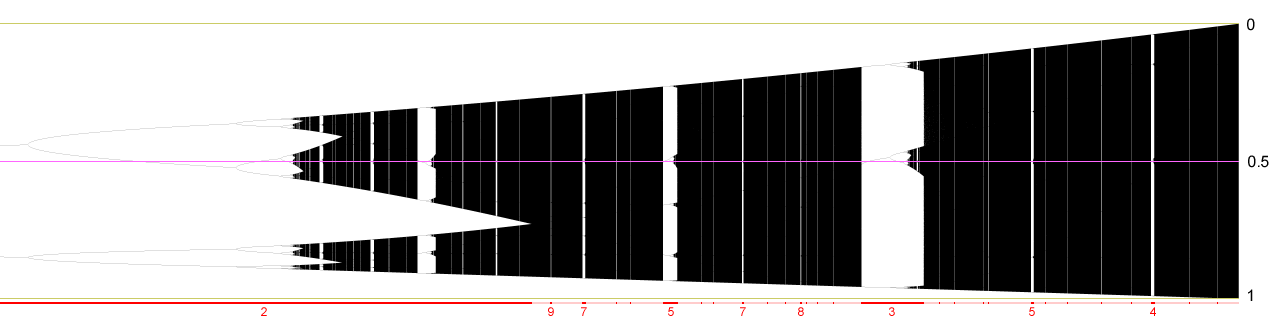
Déroulez pour la suite de l'image -->

Nous avons fait figurer les périodes associés aux plus gros de ces intervalles de paramètres. Notez qu'il n'y a qu'un seul intervalle paramétrique correspondant à la période 2. Les deux copies correspondantes de l'arbre ont leur racine en commun, et partagent un autre point commun, en leur sommet.

Plusieurs fois renormalisable

Comme la copie de l'arbre ressemble à l'arbre lui même, elle contient elle-même d'autres copies, plus petites, et ces dernières en contiennent également, etc. L'arbre est donc en quelque sorte autosemblable. Un paramètre a appartenant à une copie dans une copie est plusieurs fois renormalisable : autrement dit sa renormalisée est renormalisable.

On peut poursuivre ce procédé indéfiniment, et obtenir des paramètres a pour lesquels la fonction est dite infiniment renormalisable. Ces paramètres sont les points limites d'une suite d'intervalles emboîtés. L'attracteur de la fonction associée est un ensemble de Cantor. Un ensemble de Cantor est un type spécial d'ensemble, voir ce lien sur les ensembles de Cantor.

Cet ensemble de Cantor est l'intersection des domaines de renormalisation de chaque niveau. La figure suivante concerne une fonction f deux fois renormalisable, avec période 3 à chaque fois. On a fait figurer en rouge les carrés sur lesquels f est renormalisable, et en vert les carrés sur lesquels la renormalisée est renormalisable. (note : pour rendre la figure plus lisible, on a triché sur les tailles et les positions des carrés)

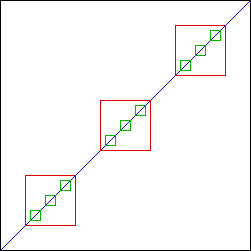
Si ce processus continue indéfiniment, on obtient une intersection de carrés de plus en plus nombreux et de plus en plus petits, qui forment un ensemble de Cantor. Il se trouve que c'est l'attracteur.

Théorème (M. Lyubich) : l'ensemble des paramètres a pour lesquels f est infiniment renormalisable est de mesure nulle.

D'autres cas ?

La réunion des intervalles paramétriques de renormalisation est dense dans [3,4], mais recouvre-t-elle entièrement ce dernier ? Non !

Théorème (Jakobson) : l'ensemble restant est de mesure positive.

Ce qui signifie que la probabilité pour qu'un paramètre pris au hasard entre 3 et 4 soit non renormalisable n'est pas nulle. Que se passe-t-il pour un tel paramètre ? L'attracteur est un intervalle I : tout point dans ]0,1[ (sauf un ensemble de mesure nulle) passe une infinité de fois arbitrairement près de tout point de I.

Les trois types de dynamique possibles

Prenons un paramètre a compris entre 1 et 4. Pour f : x ↦ a·x·(1−x), il y a deux cas

• Soit f est finiment renormalisable. Ce cas se divise en deux sous-cas : considérons la dernière renormalisée g de f et appelons h : x ↦ b·x·(1−x) la fonction de la famille de départ associée à g. (Notons que b ne peut être égal à 3 car x ↦ 3·x·(1−x) est renormalisable, de renormalisée conjuguée à x ↦ x·(1−x))
  • Soit b appartient à l'intervalle [1,3[. Dans ce cas, l'attracteur est un ensemble fini : l'orbite d'un point périodique attractif si b>1, et parabolique si b=1.
  • Soit b appartient à l'intervalle ]3,4] (notons que b n'a pas le droit d'appartenir à une fenêtre, puisque g étant la dernière renormalisée de f, g n'est pas renormalisable). Dans ce cas, l'attracteur est une union finie d'intervalles.
• Soit f est infiniment renormalisable. Alors l'attracteur est un ensemble de Cantor.