WELCOME
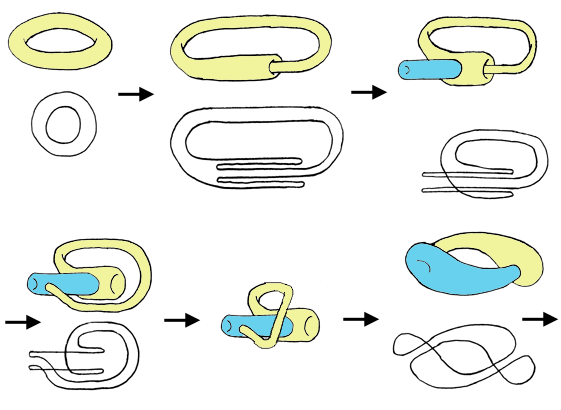
The purpose is to turn the torus inside-out i.e. to make its internal face face out and reciprocally, with the following rules: the object is a ghost , i.e. it can cross itself, it may be bent at will, but one can't fold it i.e. its curvature must be finite at every point, at last it can't be teared.
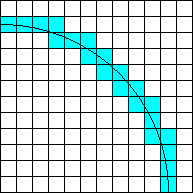There is a well known geometric method for estimating Pi: Count how many boxes of Z^2 are included in the ball of radius R,(R is a real number), and center (0,0), and divide this nuber by R^2: then the quotient tends to Pi when R tends to infinity. (it is a consequence of Area=Pi*R^2) What if one replaces the ball by the circle ? Count how many boxes the circle of radius R crosses, and divide it by 2*R (the idea is that Perimeter=2*Pi*R). Consider those of the concerned boxes which are in the first quarter of R^2, the one with equation x>0 and y>0. They form a path from the box (1,R) to the box (R,1). One can see that this path just goes right and down. (in fact it may go southeast but one shows that this happens rarely (the nuber of lost boxes divided by R tends to zero when R tends to infinity): however, just consider that the values of R are not square roots of integers so that the circle does not cross any point of the lattice Z^2, so that the path realy just goes down and right). Hence there are as many boxes as moves: R right moves and R down moves. The total is 8*R for the 4 quarters. Therefore Pi=(limit of 8R/2R when R tends to infinity)=4 Q.E.D.
More seriously, this result can be generalised for an n-dimensoinal sphere, (if you like, you can try to find the K_n constants. I can do it with elementary, non probabilistic method): let N_R the number of n-dimensional boxes crossing the n-sphere of radius R in |R^n : N_R~K_n*R^(n-1). It can be generalised to any sheet of hypersurface (not any in fact, C^1 at least) in 'position générique' (i.e. I want the sheet not to meet any corner of any box).
Let's play a game: do you have Windows 95 ? If so, take the left picture, showing concentric circles and put it as wallpaper. Then in the Start menu, choose Stop. The screen shades and... What a surprise ! New circles appeared ! But you never asked your computer to do so ?
What is that ? That's the same effect that produces moiré when shirts are filmed by cameras (those whose pixels are small compared to the distance between pixels) or during a raytracing without the antialias option. This is Aliasing.
In the pictures next to, the origin is on the lower lef corner, and one can see the concentric circles I planned to draw.
But one can also see 8 ohter families of concentric circles, that I did not invite. 3 of them are sharp, and the 5 other are more ghostly.
In these pictures, I restricted to coordinates x,y of the form n/q, where q is a fixed integer, the pattern istelf is periodic, of period P=q*q/2 if q is even. Even more: one can see many ghost circles, placed along periods of P/2, P/3, P/4, P/5, ...
Click HERE to have a big picture.
Resonance of odd order are easyer to see, because they are contrasted, contrarily to even ones.
The pictures shown here use a smooth sequence of colors : sin(Pi*frac(x^2+y^2))^2. Consequently order 2 is best visible, order 3 difficult, the other ones are beyond sight.
What happens when the picture gets grayed by Windows ? The peridicity lattice is replaced by an other, which is smaller, whose direction is 45 degrees from the starting one, and one of whose point is right in the middle of the sqare.
