Polynomial matings on the Riemann sphere

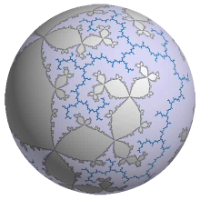
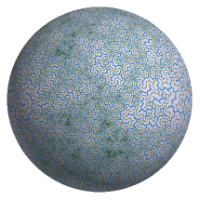
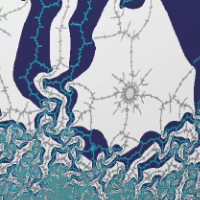
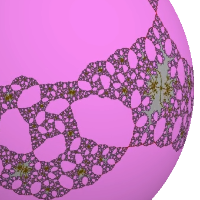
Here you will find movies of polynomial matings on the Riemann sphere.

Polynomial mating is the name given by Douady an Hubbard to a phenomenon that they discovered: the Julia sets of some rational maps is homeomorphic to the gluing of two filled-in polynomial Julia sets along their boundaries, by a gluing that respects the marking by external angle and thus the corresponding dynamical systems on the Julia sets.

A progressive interpolation was introduced, between the two polynomial Julia sets and their mating. It consists in gluing equipotentials together and gives a holomorphic dynamical system between different spheres (this was observed by Milnor). This dynamical systems gives an easy method for drawing a conformally correct picture of the deformation of the polynomial Julia sets under the equipotential gluing: this method was explained to me by Buff. The result is an image which depends on the potential. This is what the movies show: the potential starts high and slowly approaches 0.

Rabbit|Basilica	Rabbit|Rabbit	Rabbit|Kokopelli	Rabbit|Airplane
Rabbit|Dendrite 1/6	Rabbit|Dendrite 1/4	Dendrites: 1/4|1/4	Dendrites: 1/4|1/6
Dendrites: 1/6|5/14	Airplane|Dendrite 1/4	Airplane|Kokopelli	Long ray connect
Shared	Siegel|Siegel	Magic	Newton (deg 3)
Pacman!	Deg 3, non-Lev obstr	Dendrites: 5/12|1/12	Dendrites: 1/6|1/6
Tuning