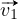 et
et 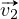 les vecteurs supportés par les arêtes adjacentes à B et orientées du
moins (−) vers le plus (+). Le cône CB est engendré par les vecteurs
les vecteurs supportés par les arêtes adjacentes à B et orientées du
moins (−) vers le plus (+). Le cône CB est engendré par les vecteurs 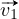 et
et
 :
:
Quels angles (solides) définis par un tétrèdre peut-on sommer pour obtenir une quantité invariante ?
Le but de cette page est de décrire une réponse possible. Plus généralement, pour un simplexe de dimension \(n\) fixée, nous décrivons une façon de rendre invariante la somme des mesures d'une collection d'angles (solides de dimension \(n\)) définis par le simplexe.
En géométrie euclidienne, dans le plan, on a l’énoncé vernaculaire suivant :
Théorème 1 La somme des angles d’un triangle fait toujours π radians (et 180 degrés).
En dimension trois, la somme des angles (solides) aux sommets d’un tétraèdre,
en revanche, n’est pas constante. Le but de cette page est d’exposer une
généralisation, aux trétraèdres et à n’importe quel simplexe de dimension n
supérieure ou égale à deux, de l’énoncé pour les triangles. C’est relativement
évident et il est probable que ce soit bien connu depuis l’antiquité ou du moins de
longue date. Nous sommes tombés dessus par hasard en écrivant
« On the Total Curvature of Tropical Hypersurfaces » (B. Bertrand, L. López de Medrano et J.-J. Risler) publié dans « Algebraic and Combinatorial Aspects of Tropical Geometry, AMS Contemporary Mathematics 589 » qu'on peut trouver grosso modo ici.
Les remarques et références
sont les bienvenues.
La mesure de l’angle solide en un sommet B d’un tétraèdre n est l’aire de l’intersection du cône engendré par les arêtes issues de B et de la sphère unité centrée en B.
Commençons par redémontrer que la somme des angles d’un triangle euclidien
est π radians. Nous montrons en fait que l’on peut réarranger les cônes
engendrés par les arêtes du triangle pour qu’ils pavent un demi-plan.
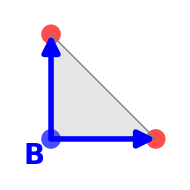
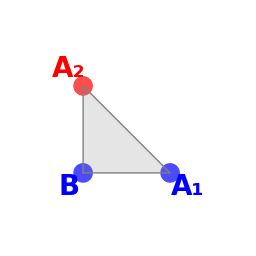
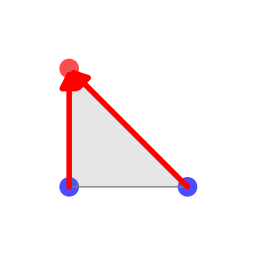
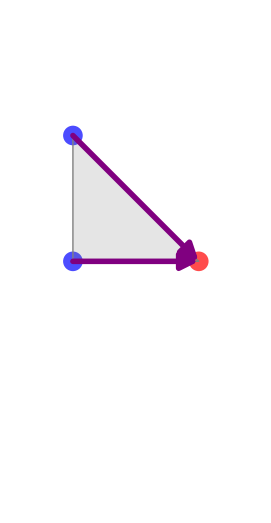
Choisissons un des sommets du triangle que nous nommerons B et équipons-le
d’un signe moins (−) fixé une fois pour toute, représenté par la couleur bleue sur
les illustrations. Considérons le cône CB de sommet B engendré par les arêtes
du triangle adjacentes à B. Étiquetons d'abord les deux autres sommets
du triangle par plus (+) représenté par la couleur rouge. Soit 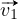 et
et 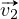 les vecteurs supportés par les arêtes adjacentes à B et orientées du
moins (−) vers le plus (+). Le cône CB est engendré par les vecteurs
les vecteurs supportés par les arêtes adjacentes à B et orientées du
moins (−) vers le plus (+). Le cône CB est engendré par les vecteurs 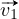 et
et
 :
:
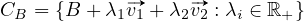
.
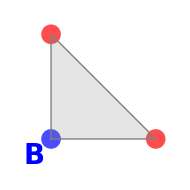 |  |  |
| Triangle avec un signe moins | Arêtes orientées de moins vers plus | Cône engendré par les arêtes |
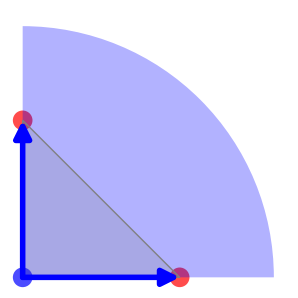
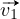 et
et 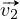 a même mesure que l’angle
en B du triangle.
a même mesure que l’angle
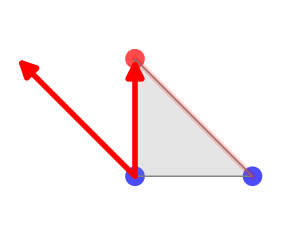
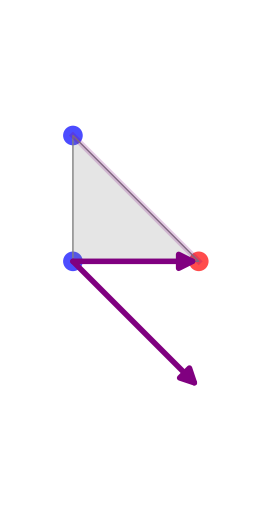
en B du triangle. Étiquetons maintenant un autre sommet, disons A1, par moins (−) et le dernier,
disons A2, est étiqueté par plus (+) alors que B reste toujours équipé
d’un moins (−). Les vecteurs 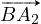 et
et 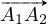 engendrent le cône de sommet
B,
engendrent le cône de sommet
B,
 |  |  |  |  |
Triangle avec deux signes moins et un plus | Arêtes orientées de moins vers plus | Vecteurs représentés avec origines en B | Cône engendré | Cône engendré |
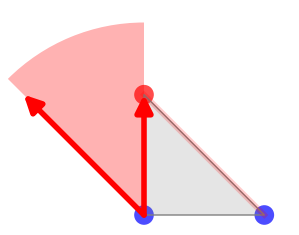
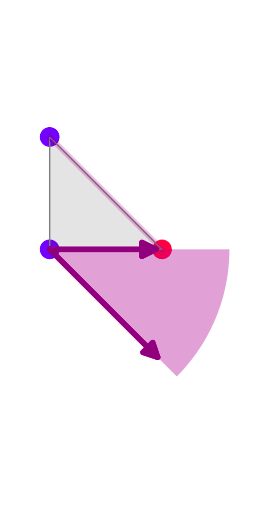
L’angle (non-orienté) défini par les vecteurs 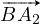 et
et 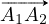 a même mesure que
l’angle en A2 du triangle.
a même mesure que
l’angle en A2 du triangle.
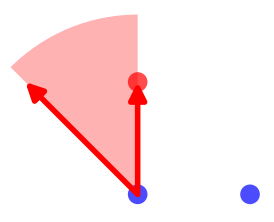
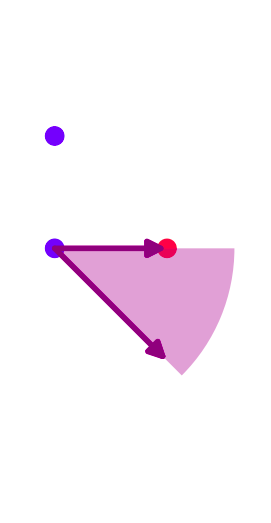
De même, en étiquetant A2 par moins (−) et A1 par plus (+), on obtient le cône
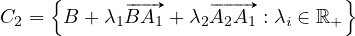
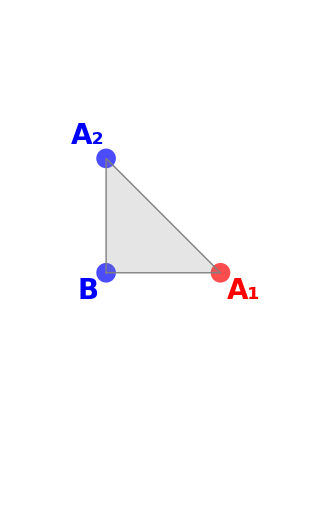 |  |  |  |  |
Triangle avec deux signes moins et un plus | Arêtes orientées de moins vers plus | Vecteurs représentés avec origines en B | Cône engendré | Cône engendré |
L’angle (non-orienté) défini par les vecteurs 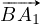 et
et 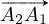 a même mesure que
l’angle en A1 du triangle.
a même mesure que
l’angle en A1 du triangle.
Les trois cônes CB,C1 et C2 pavent un demi-plan. La somme des mesures de leurs angles est donc la mesure d’un demi-cercle unité.
Les cônes ainsi obtenus pavent un demi-plan.
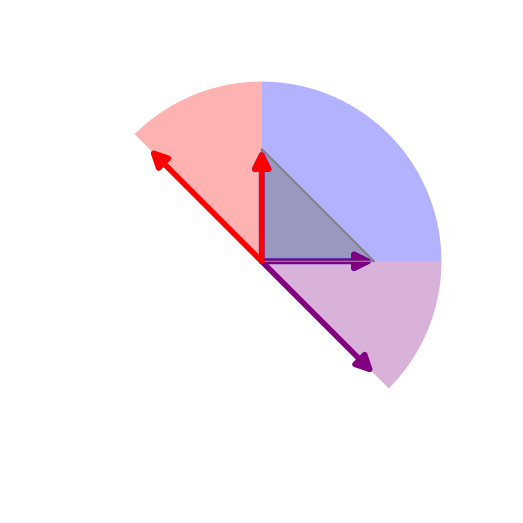
Les angles des cônes correspondant aux angles du triangle, on a redémontré que la somme des angles d’un triangle mesure π radians.
Passons maintenant aux dimensions supérieures. On fera les illustrations sur un tétraèdre mais cela fonctionne pour n’importe quel simplexe de n’importe quelle dimension n supérieure ou égale à 2. Le texte ci-dessous peut se lire en remplaçant n par 3 et donnera alors une généralisation pour les tétraèdres de l’énoncé pour le triangles.
On va appliquer exactement le même algorithme que pour notre preuve de la somme des angles d’un triangle.
Rappelons que la mesure de l’angle solide en un sommet B d’un simplexe de dimension n est le volume de l’intersection du cône engendré par les arêtes issues de B intersecté avec la sphère unité de dimension n − 1 centrée en B.
Voici l’énoncé en dimension 3 :
Théorème 2 (Angles issus d’un tétraèdre) La somme des angles solides obtenus d’un tétraèdre avec la procédure décrite ici est 2π stéradians (c’est à dire l’aire d’une demi-sphère unité).
Et en dimension quelconque :
Théorème 3 (Angles issus d’un simplexe) La somme des angles obtenus d’un simplexe de dimension n avec la procédure décrite ici est le volume d’une demi-sphère unité de dimension n − 1.
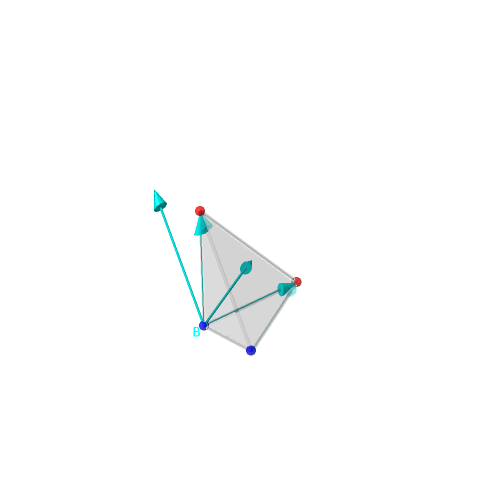
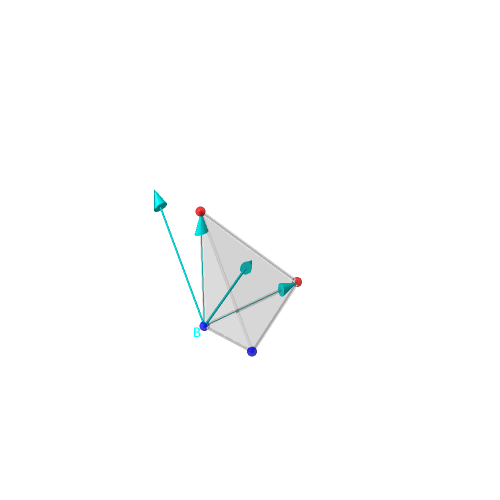
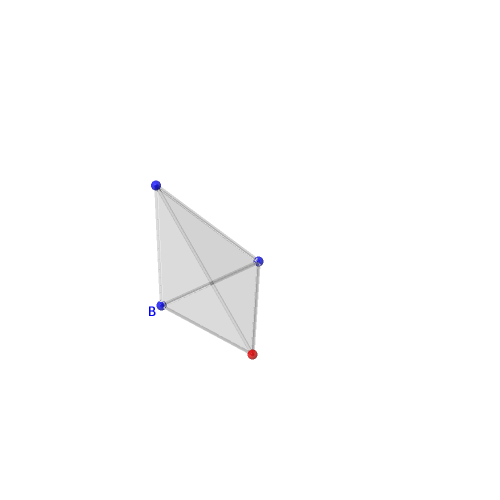
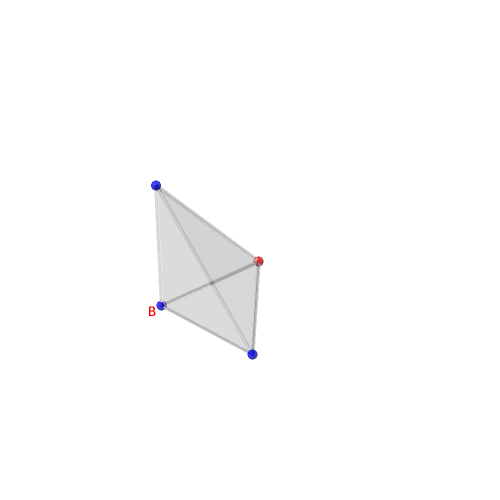
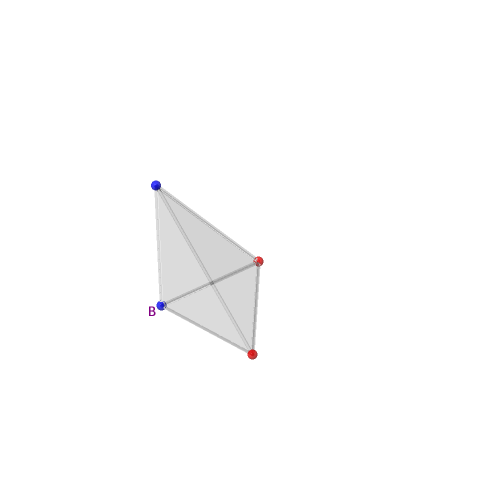
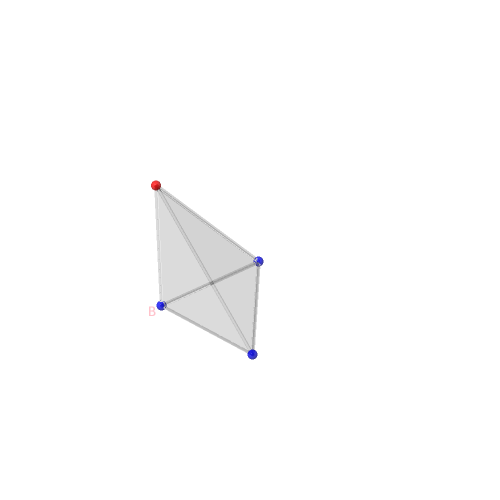
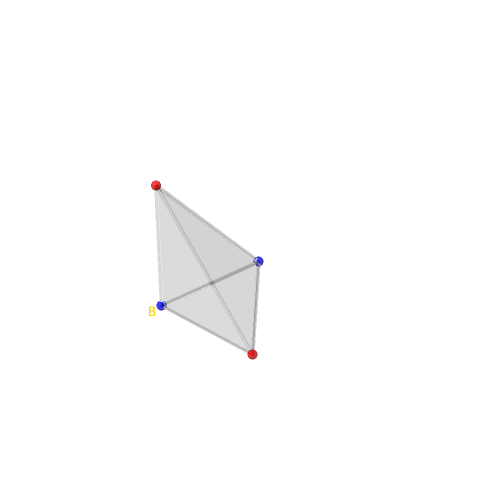
Choisissons un des sommets du simplexe que nous nommerons B et équipons-le d’un signe moins (−) fixé une fois pour toute, représenté par la couleur bleue sur les illustrations.
Pour les autres sommets, on considère une à une toutes les configurations σ de
signes possibles. À un choix de signes σ sur chaque sommet, on associe les arêtes
bipolaires orientées de moins (−) vers plus (+). Les vecteurs définis par ces
arêtes orientées engendrent un cône Cσ.
Exemple de cette construction avec σ composée uniquement de plus (+) un cône simplicial (engendré par une base de ℝn).
| Tétraèdre -- Seul B a un signe moins (bleu) | Arêtes orientées | Tétraèdre, vecteurs et cône | Vecteurs et cône |
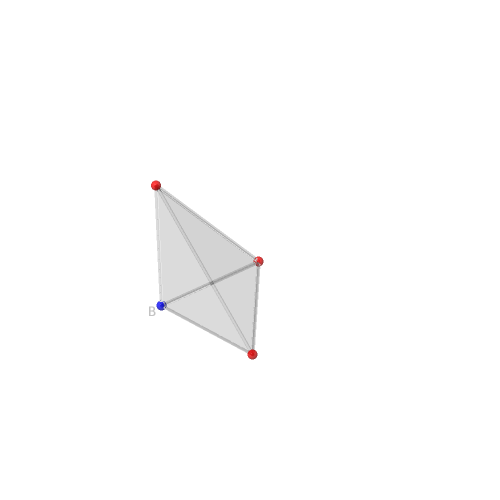 |
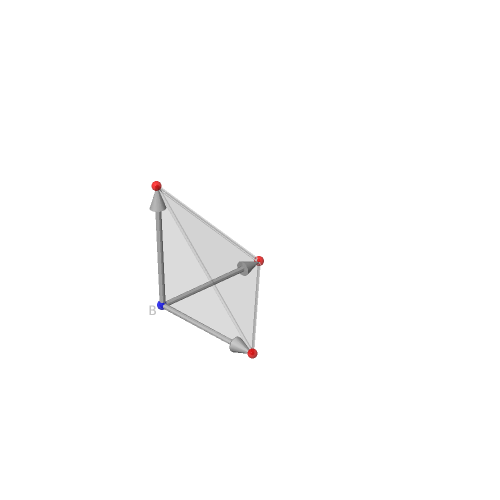 |
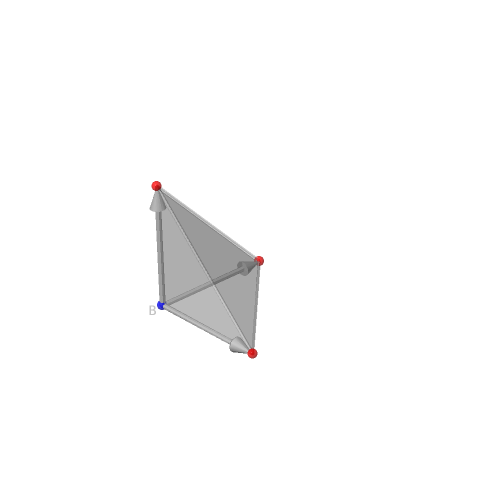 |
 |
Les deuxième et troisième lignes de la table ci-dessus sont cliquables pour obtenir la vue interactive pleine page.
| tétraèdre et signes sur les sommets | arêtes orientées | on place l'origine des vecteurs en B | vecteurs engendrant le cône | tétraèdre, vecteurs et cône | vecteurs et cône |
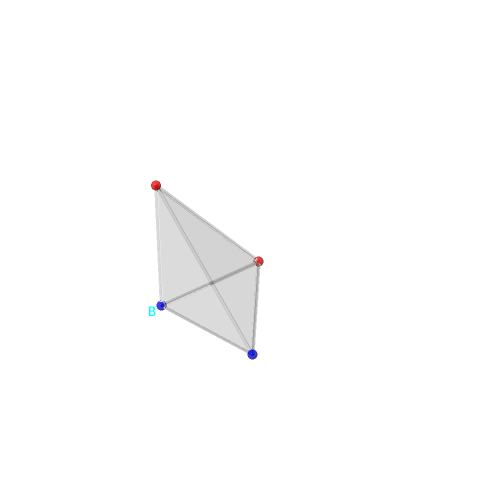 |
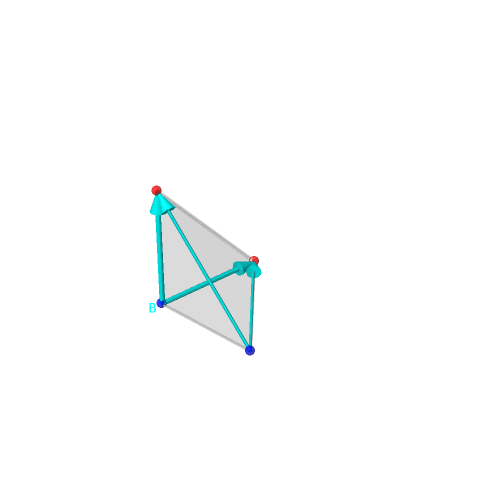 |
 |
 |
 |
 |
Les deuxième et troisième lignes de la table ci-dessus sont cliquables pour obtenir la vue interactive pleine page.
 |
 |
 |
 |
 |
 |
 |
|
En sélectionant des distributions de signes ci-dessous (en dimension 3) on obtient les tronçons de cônes correpondants et leur arrangement dans le cadre en dessous. On peut ainsi repérer leur positions relatives
 |
 |
 |
 |
 |
 |
 |
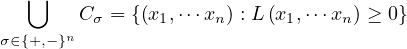
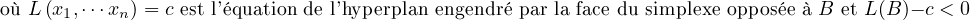
ci-dessous une visualisation des 7 cônes obtenus en dimension 3
Les 2n − 1 cônes obtenus pavent un demi-espace DB. L’angle solide correspondant mesure une demi-sphère de dimension n − 1.
Remarque 1 Si on relaxe la condition sur le signe de B (i.e. on autorise B à prendre le signe plus (+)) on obtient bien-sûr un pavage de l’espace et une somme des mesures des angles décrits double (correspondant au volume d’une sphère).
Le demi-espace DB est délimité par l’hyperplan vectoriel parallèle à l’hyperplan affine engendré par FB la face du simplexe opposée à B. Le fait que les vecteurs engendrés par les arêtes orientées contenues dans la face FB est donné par l’énoncé en dimension n − 1.
Les cônes adjacents à une arête a du simplex considéré contenant B (i.e. non contenue dans sa face opposée FB) sont obtenus en fixant le signe du deuxième sommet de l’arête a à plus (+) et en faisant varier les autres signes. Ils recouvrent un voisinage du rayon engendré par a.
Pour le voir, nous pouvons par exemple remarquer que le simplexe avec un sommet marqué (B) détermine une base de ℝn. Les faces de dimension n − 1 contenant B engendrent les hyperplans de coordonnées dans cette base. Ils découpent ℝn en 2n chambres coniques. Les 2n−1 qui contiennent l’arête a réalisent un pavage d’un voisinage d’icelle. Un point proche du rayon engendré par a est dans le cône donné par la distribution de signes correspondant aux signes de ses coordonnées dans la base décrite. C'est à dire qu'il suffit de prendre pour chaque sommet Ai du simplexe qui n'est pas dans l'arête a le signe qui est celui de la coordonnée du point sur l'axe le long du vecteur \(\overrightarrow{BA_i}\). Il n’y a donc pas de « trous » dans le pavage !
Plus généralement nous pouvons ainsi décrire l’étoile de n’importe quelle face du complexe polyédral donné par l’algorithme spécifié ci-dessus et nous avons prouvé que ces cônes réalisent bien un pavage du demi-espace. En particulier, la somme des mesures angles solides des cônes est bien égale à la mesure d’une demi-sphère.
Remarque 2 On peut trianguler n'importe quel polytope convexe en simplexes dont les sommets sont tous des sommets du polytope. On peut bien-sûr appliquer la construction précédente à chaque simplexe et obtenir comme angle total le produit du nombre de simplexes par le volume d'une demi-sphère unité. Le problème est que ce nombre n'est pas constant. On peut par exemple trianguler un cube avec 5 ou 6 tétraèdres suivant que l'un d'eux est le joint de deux diagonales de direction différentes sur deux faces parallèles ou pas. En se restreignant aux polytopes à sommets entiers, et à leur triangulations primitives (dont les simplexes ont tous volume \(\dfrac{1}{n!}\)) quand ils en admettent, on obtient alors que l'angle total est \(n!\) fois le produit du volume du polytope par le volume d' une demi-sphère unité (de dimension n-1).