Polynomial matings on the Riemann sphere

Rabbit with Basilica

This is the historical example.

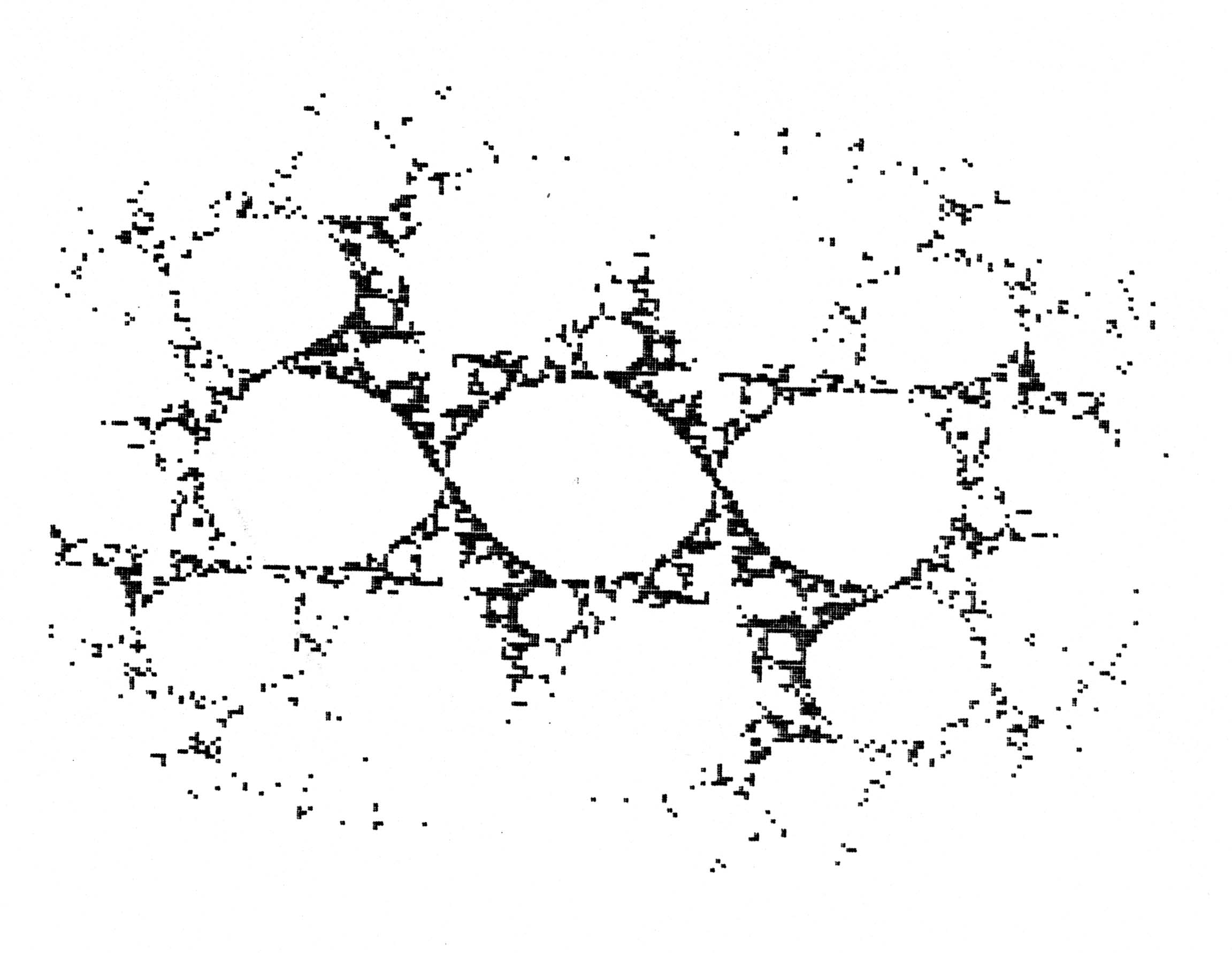
The picture above is part of a numerical experient carried-out by Douady and Hubbard in the 1980's. They were computing rough pictures of the Julia sets of all post critically finite degree 2 rational maps with a given bound on the size of post critical set. Looking at the picture above Douady and Hubbard recognized the gluing of the filled in Julia sets of two post-critically finite degree polynomials they were quite familiar with; they had even given them nicknames: the Basilica and the Rabbit.

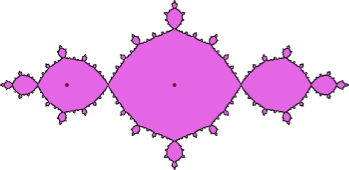← Basilica Rabbit →

And above you can see a more detailed picture of the Julia set, drawn on the complex plane. The rational map has two critical points, 0 and infinty. The point 0 has period 2 and infinity has period 3. Their orbits are indicated by red dots (the one at infinity is not visible).

Since then, it has been proved in a precise way that the Julia set is indeed the mating of the basilica and the rabbit.

Below: the so-called slow mating.

You can also download:

• The movie above (mp4, 3.5MB)
• The movie, with external rays added, faster (mp4, 1.7MB)
• Another view (wmv, 5.9MB) with the critical points at the north and south poles.
• Hemispheres only (wmv, 536KB)