Modular hyperbolic tilings
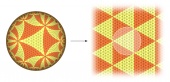
A 12 colors tiling related to the usual subgroup of the modular group, highlighting the 3 cusps
Another colouring of the same picture; the union of the 2 biggest visible tiles form the standard fundamental domain
A conformal grid growing from the 'spine'
Higher resolution
The image of the coulouring scheme by the (pre)modular function
Higher resolution
Modular hyperbolic tilings, black and white
Tesselation by some fundamental domain for the modular group (high resolution)
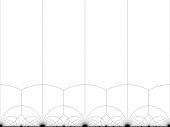Another fundamental domain
Yet another
A fundamental domain for an index 2 subgroup
A fundamental domain for an index 3 subgroup
A fundamental domain for an index 6 subgroup
A fundamental domain for a coindex 2 supgroup
Klein's quartic. A very symmetric complex-curve (a.k.a. Riemann surface) in P2C.
Klein told us: glue this fundamental domain the right way (2 solutions, not so obvious), and you'll get a very symmetric Riemann surface.
Ahlfors and Grunsky's conjectural optimal function for Bloch's constant
Topology
Surfaces of genus 1, 2 and 3
Measure preserving maps
Agate?
Mixing
Mixing on the sphere
Hypnose
Polytopes
Three patterns of the 24-cell
Three patterns of the 24-cell
Some patterns
Écorché de l'ombre du 120
An Archemedean polytope
The Runcinated 120-cell is a polytope. It is Archimedean in the sense that its organization at every vertex is the same, and all its chambers are Archimedean polyhedra too: regular dodecahedra, prisms with regular pentagonal base and square sides, prisms with equilateral triangular base and square sides, and regular tetrahedra. Here, these objects are respectively represented green, purple, yellow and orange. To represent the object, it is projected orthogonally to the three dimensionnal space and then rendered into a 2D image. We used LuxRender for a photorealistic look.
Click here for more information
The outer shell is made of flattened cells and completely encloses the interior. We broke the shell to reveal cells below.
Same, without the outer shell. The cells are shrunk a little bit, to enhance visibility.
By accident, some groups of cells are neatly separated by planes.
Undraping the polytope
...
...
...
...
...
...
Showing only tri-prisms
The dual of the polytope
A view of the inside
Dodecahedral fundamental domain of the Seifert-Weber hyperbolic space
The set, sitting in the ball model of hyperbolic space.
The domain is the intersection of half-spaces bounded by hyperbolic planes
Looks like a flower
A Kleinian reflection group with a Sierpinski limit set
The group is generated by the reflections along the 4 blue circles. Black: limit set. Yellow tones: generated tesselation in the discreteness set.
They are arranged so as to have a tetrahedral symmetry and so that they intersect at angle a turn / 7
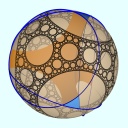An index 24 subgroup has the following tetrahedral fundamental domain
A cubemap if you want to play with a visualizing tool
well... if your tool accepts cube maps
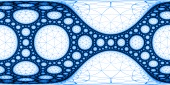A spheremap
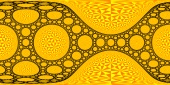... if you manage to find a visualizing tool
Sphere viewer
In fact, I have written a viewer: test it on the links here and here
A non geometrically finite end of a finite type Kleinian group
Fundamental domain for an hyperbolic structure of an Anosov suspension of a punctured torus
Boy's surface
Boy's surface is a non-orientable self-intersecting surface, it is also an immersion of the projective space RP2 into R3
Click here for more information
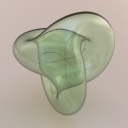Boy's surface, transparent
Boy's surface, semi-transparent, cut open
Solenoid
A solenoid can refer to different things. Here it is a particular subset of R^3 that is homeomorphic to some projective limit of the reals mod 1, R/Z, under doubling. It is also obtained as the attractor of a particular map that sends some solid torus injectively inside itself, winding twice.
A solenoid
A more metallic shine
Sections are Cantor sets