Points fixes

On appelle cycle une chaîne de points envoyés chacun sur le suivant, et qui boucle : x₀ ↦ x₁ ↦ x₂ ↦ … ↦ x_n = x₀ C'est une propriété de la famille x ↦ a·x·(1−x) qu'il n'y a jamais plus d'un cycle attractif (alors qu'il y a des fonctions qui en ont plusieurs).

Quand l'attracteur est constitué d'un cycle attractif, ce qui n'est pas toujours le cas, les points d'un cycle répulsif ne peuvent être attirés, ce sont donc des exceptions (ainsi que tous les points qui finissent par tomber sur un des points du cycle répulsif, ce que l'on nomme les images réciproques)

Les points fixes de la famille a·x·(1−x)

Les cycles les plus simples sont les cycles de période 1, c'est à dire les points fixes. Trouver les points fixes, c'est trouver les nombres x tels que le suivant, f(x), soit égal à x, donc cela revient à résoudre l'équation

f(x)=x

C'est à dire

a·x·(1−x)=x

Il y a un méthode standard pour résoudre ce genre d'équation : elle équivaut à

a·x·(1−x) − x = 0

à

x·(a·(1−x)−1) = 0

à

x=0 ou a·(1−x)−1 = 0

à

x=0 ou a·(1−x) = 1

Si a=0, alors seul x=0 est fixe. Sinon, l'équation équivaut à

x=0 ou (1−x) = 1/a

à

x=0 ou x = 1 − 1/a

Donc les points fixes sont 0 (que l'on connaissait déjà) et 1−1/a quand a est non nul. Mais attention ! Le point 1−1/a n'est compris entre 0 et 1 que quand a est plus grand que 1.

Comment savoir si le point fixe est attractif ? Avec la dérivée. Si vous ne savez pas ce que c'est, aucune importance, passez à la page suivante. Sinon, on calcule que

f'(x) = a·(1 − 2·x)

Donc la dérivée en 0 est égale à

f'(0)=a

et la dérivée en 1−1/a à

f'(1−1/a)=2−a

La dérivée de f en x représente la pente du graphe au point x, et on a vu que le point était attractif quand la pente est comprise entre -1 et 1. Quand elle vaut -1 ou 1, on dit que le point est neutre :s c'est un cas particulier que nous ne traiterons pas ici. Quand elle est de valeur absolue >1, il est répulsif.

Donc 0 est attractif quand 0<a<1, et répulsif quand 1<a<4. Quand à 1−1/a, il est attractif quand 1<a<3 et répulsif quand 3<a (rappelons que quand 0<a<1, 1−1/a n'est pas dans l'intervalle [0,1]).

Conséquences pour l'arbre de Feigenbaum

Reprenons le dessin de l'arbre, en superposant les points fixes, dessinés en vers quand ils sont attractifs et en rouge quand ils sont répulsifs.

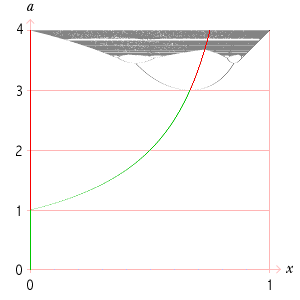
Testez la méthode de l'escalier/escargot pour x ↦ a·x·(1−x) avec l'applet suivant.