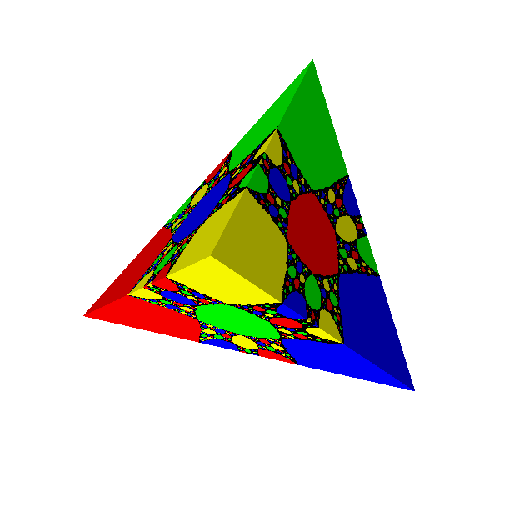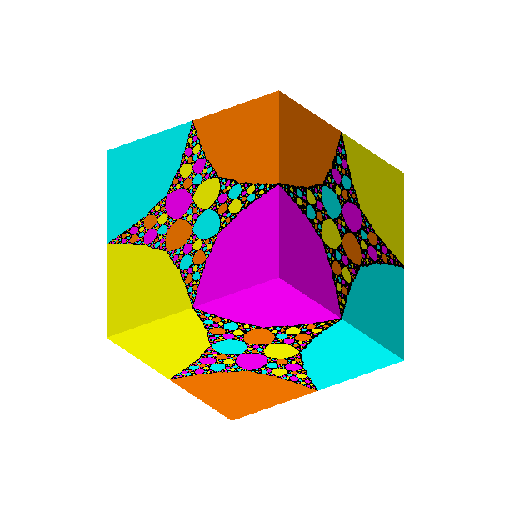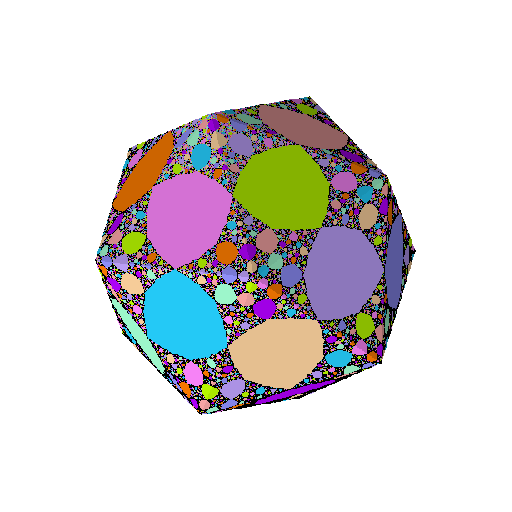Rational maps with symmetries
The group of automorphisms Aut(f) of a rational map f:P1->P1 of degree d>1
is defined to be the group of Moebius transformations that commute with
that rational map. When Aut(f) is not trivial, we say that f is a rational map with symmetries. The group Aut(f) is a finite subgroup of PSL(2,C). Such groups are classified; up to conjugacy by an automorphism of P1, Aut(f) is either:
-
trivial, or
-
the cyclic group generated by the rotation of angle 1/kth
of a turn centered at 0
- in that case, f is of the form z->zg(zk), where
g is any rational map - or
-
the dihedral group generated by the rotation of angle 1/kth centered at 0 and by the Moebius transformation z->1/z - in that case, f is of the form
z->±z1-nkP(zk)/P(1/zk),
where P is any polynomial and n is an integer- or,
-
the group of symmetries of a tetrahedron, or
-
the group of symetries of a cube (and by duality of an octahedron), or
-
the group of symmetries of a dodecahedron (and by duality of an icosahedron).
Any finite subgroup G of PSL(2,C) can be realized as the
group of automorphisms of some rational map (see [Doyle-McMullen, Solving
the quintic by iteration]). There are lots of rational maps f
for which Aut(f)=G but the set of such rational maps has very few isolated
points. We say that such isolated points are rigid rational maps with
symmetries.
-
When G is a cyclic group, there are no rigid rational maps.
-
When G is the dihedral group generated by the rotation of angle 1/kth centered
at 0 and by the Moebius transformation z->1/z, the only rigid rational maps
with Aut(f)=G are z->±1/zk-1.
-
When G is the group of symmetries of a tetrahedron, there are three rigid
rational maps with Aut(f)=G: two of them are Lattès examples, the
third one is a post-critically finite hyperbolic rational map.
-
When G is the group of symmetries of a cube or an octahedron, there are
three rigid rational maps with Aut(f)=G; they are hyperbolic and post-critically
finite.
-
When G is the group of symmetries of a dodecahedron or an icosahedron,
there are three rigid rational maps with Aut(f)=G; they are hyperbolic
and post-critically finite.
The following pictures show the Julia sets of those hyperbolic and post-critically finite rigid rational maps with symmetries, radially projected from the Riemann sphere onto the Platonic solid whose group of symmetries coincide with Aut(f). By clicking on the picture,
you will get a picture of the Julia set drawn on the sphere and an enlargement of
the projection onto the Platonic solid. You may then get a pdf-file of a pattern that you can cut and paste.
You may also download directly all the patterns in a pdf-file patterns.pdf or in a compressed postscript file patterns.ps.gz (the size of the patterns is suitable for printing on A4 paper).