 Julia set of z->(exp(z)-1)/2
Julia set of z->(exp(z)-1)/2
 |
| Closeup of the Julia set of z->(exp(z)-1)/2 |
 |
| High resolution (for inkjet printers) |
 987 petals
987 petals
 |
| A quad. Julia set with 987 parab. petals in approx. Fatou coord. |
 The cauliflower
The cauliflower
 |
| Colorful cauliflower |
 |
| Checked towel cauliflower filling |
 Quad. poly. with a parabolic fixed point with many petals
Quad. poly. with a parabolic fixed point with many petals
 |
| 13/34 rot. nb. ind. fix. pt. Julia set. |
 |
| (hi res) |
 |
| 34/89 |
 |
| (hi res) |
 Golden mean Siegel disk
Golden mean Siegel disk
 |
| Golden mean Siegel disk |
 |
| (hi res) |
 |
| Closeup on the critical point of the golden mean quadratic Siegel disk |
 |
| (hi res) |
 |
| Approx. domain of def. of the McMullen limit map |
 |
| (hi res) |
 Quasiconformal models
Quasiconformal models
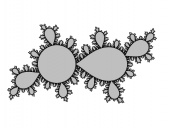 |
| Ghys model for the quad. gold. mean Sieg. disk. |
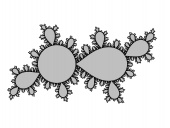 |
| (hi res) |
 |
| Full Julia set of the previous Blaschke fraction. |
 |
| (hi res) |
 Virtual Siegel disks
Virtual Siegel disks
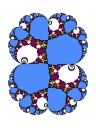 |
| Virtual Siegel disk in the cauliflower |
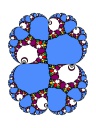 |
| (hi res, color) |
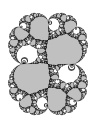 |
| (lo res, grayscale) |
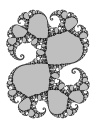 |
| Siegel disk tending to the previous |
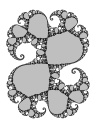 |
| (hi res) |
 |
| Virtual Siegel disk in the 2/5 rabbit |
 |
| (hi res) |
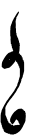 Pérez-Marco's Riemann sufaces
Pérez-Marco's Riemann sufaces
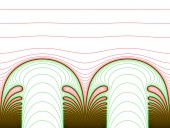 |
| Uniformization of Pérez-Marco's tube-log Riemann surface |
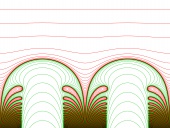 |
| (hi res, color) |
 |
| (lo res, grayscale) |
 |
| (hi res, black and white) |
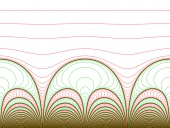 |
| Uniformization of another Riemann surface of Pérez-Marco |
 |
| (hi res, color) |
 |
| (lo res, grayscale) |
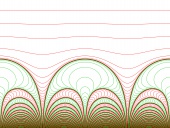
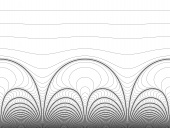 |
| (hi res, black and white) |
 Siegel disk of exp(z)+c
Siegel disk of exp(z)+c
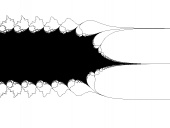 |
| The golden mean fixed Siegel disk in the family exp(z)+c (lo res, grayscale) |
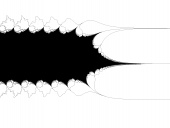 |
| (hi res, black and white) |
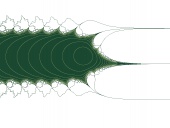 |
| Plus some of its invariant circles (medium, color) |
 |
| (hi res, color) |
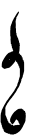 Digitated Siegel disk
Digitated Siegel disk
 |
| Digitated Siegel disk |
 Zakeri's Jordan curve
Zakeri's Jordan curve
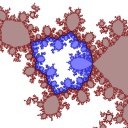 |
| Zakeri's Jordan curve in a slice of the parameter space of cubic polynomials |
 Pseudo hedgehogs
Pseudo hedgehogs
 |
| A pseudo hedgehog |
 |
| Another |
 |
| Another |
 |
| Another |
 |
| Another |
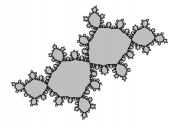
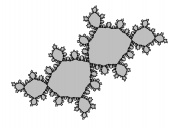
 Near matings
Near matings
 |
| Two mating polynomial Julia sets |
 |
| Close-up on the previous one |
 |
| Douady's rabbit mating with a dendrite |
 Near tunings
Near tunings
 |
| Tuning a dragon by a segment |
 |
| ... closer to the limit |
 A disconnected rational Julia set
A disconnected rational Julia set
 |
| A disconnected rational Julia set |
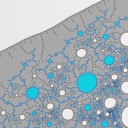
 Bifucation loci in parameter spaces
Bifucation loci in parameter spaces
 |
| Mandelbrot sets everywhere |
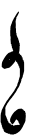 A Julia set equal to the Riemann sphere, looks like Jupiter's moon Callisto
A Julia set equal to the Riemann sphere, looks like Jupiter's moon Callisto
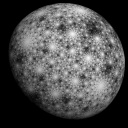 |
| A representation of the invariant measure associated to some post-critically finite rational map whose Julia set is the whole sphere. |
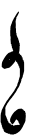 Three representations of the same Julia sets with a Herman ring: z+a*sin(z)+t, with golden mean rotation number.
Three representations of the same Julia sets with a Herman ring: z+a*sin(z)+t, with golden mean rotation number.
 |
| Julia set with a Herman ring |
 |
| Same Julia set, shades of gray revealing more structure |
 |
| Another representation |
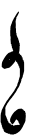 Parabolic renormalization
Parabolic renormalization
 |
| Shishikura's invariant class |
 |
| exp |
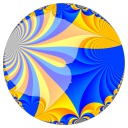 |
| tan |